Umetnost in matematika - Kako risanje pomaga pri razvoju matematičnih veščin

Na prvi pogled se umetnost in matematika zdita kot dve popolni neznanki in popolnoma različni področji. A ko se poglobimo, lahko ugotovimo, da sta tesno prepleteni, še posebej ko gre za risanje.

Na prvi pogled se zdi, da je matematika skupek abstraktnih pojmov in enačb, medtem ko je umetnost izrazno področje, ki ga povezujeta domišljija in ustvarjalnost.

Ko se poglobimo v to področje, vidimo, da se matematika in umetnost, čeprav na videz nasprotujoča, tesno prepletata. Matematika je osnova, ki omogoča umetniško izražanje. Ta odnos je tudi skozi zgodovino vplival na dela znanih umetnikov, arhitektov in oblikovalcev ter neopazno oblikoval naš vizualni svet. In danes ni nič drugače.

Vir: mathcreativity.com

Risanje je vsekakor večplastno, saj je po eni strani ustvarjalno izražanje, je pa med drugim tudi učinkovit način za razvijanje matematičnih veščin pri otrocih. Skozi geometrijo, simetrijo, perspektivo in še več odkrivamo skrito prepletanje teh dveh področji in ustvarja most med logiko in domišljijo.

Tukaj je nekaj ključnih načinov, kako risanje pomaga otrokom pri učenju matematike:

Geometrija in oblike - Risanje bo spodbudilo vašega otroka k raziskovanju različnih oblik in vzorcev. Ko otroci rišejo trikotnike, kvadrate, kroge ali druge, bolj zapletene oblike, se nezavedno učijo osnov geometrije. Krogi, kvadrati, trikotniki in drugi večkotniki so osnova za ustvarjanje najrazličnejših oblik v dvodimenzionalni in tridimenzionalni umetnosti. Risanje kompleksnejših vzorcev, kot so na primer MANDALE, pomaga otrokom razumeti pojme, kot so simetrija, sorazmerje in geometrijski odnosi.

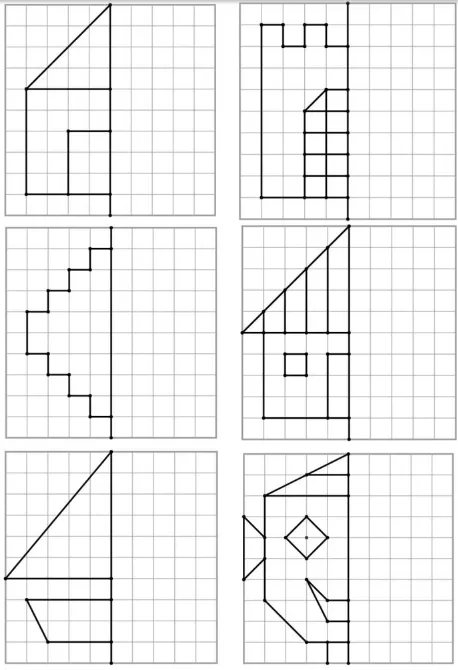
Merjenje in prostorska zaznava - S tem, ko otroci rišejo predmete ali prizore, trenirajo svojo sposobnost določanja velikosti, razmerja in položaj predmetov na papirju. To pa močno spodbuja njihove prostorske sposobnosti in sposobnost merjenja. V to pa je vključeno tudi učenje o perspektivi, kjer so bližnji predmeti večji, oddaljeni pa manjši.

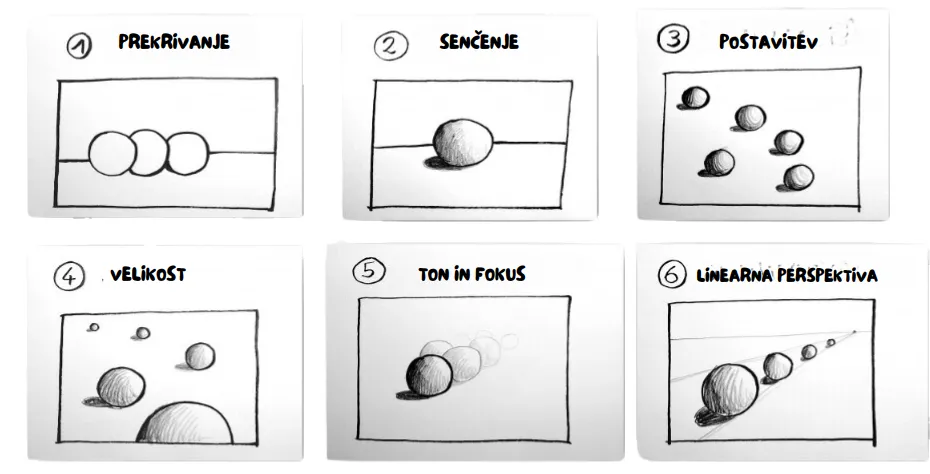
6 načinov kako ustvariti iluzijo prostora na papirju (vir: arteascuola.com)

Vzorci in sekvence - Ustvarjanje vzorcev skozi risanje je zabaven način za uvajanje matematičnih konceptov. Otroci lahko rišejo ponavljajoče se vzorce z različnimi barvami in oblikami, kar jih uči o sekvencah, ritmu in zaporedjih – le ti pa so osnova za razumevanje matematičnih funkcij in algoritmov.

Simetrija - Simetrija je ključni koncept v matematiki, zlasti v geometriji. Ko otroci rišejo simetrične slike, kot so metulji ali obrazi, se učijo prepoznavati in ustvarjati simetrične vzorce. To krepi njihovo razumevanje osi simetrije in jih pripravlja na bolj zapletene matematične pojme, kot je simetrična funkcija - saj veš leva stran enačbe = desna stran enačbe.

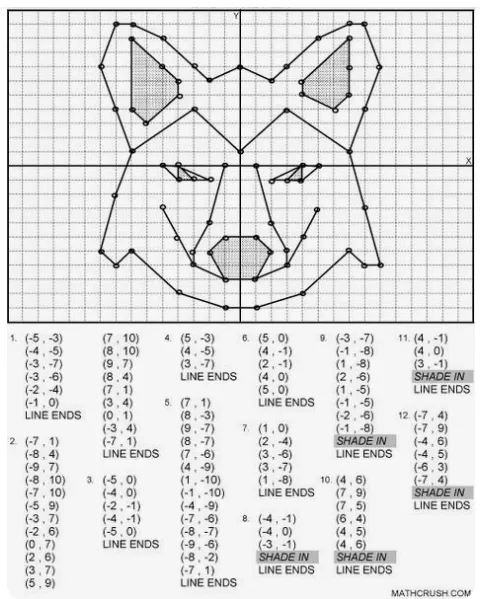
Koordinatni sistem - Risanje na mrežastem papirju je v bistvu kot risanje v koordinatnem sistemu in je bolj nežen uvod v osnovne pojme algebre in geometrije. S tem, ko otroci določajo točke na mreži ali rišejo grafe, se učijo o koordinatnih sistemih in povezovanju točk, kar pa jim zelo pomaga izboljšati matematično natančnost.

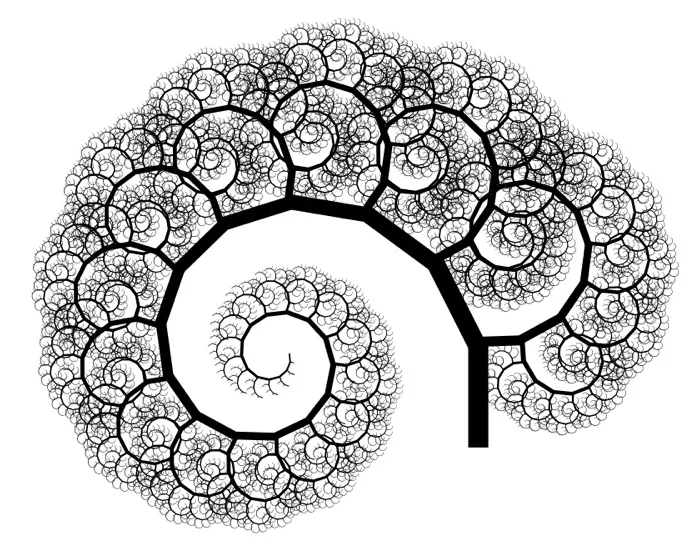
Fraktali in kompleksni vzorci - Fraktali so matematične oblike in imajo lastnost, da so si podobni na različnih ravneh povečave – vsak manjši del fraktala ponavlja vzorec celote. Raziskovanje fraktalov skozi risanje lahko starejšim otrokom ponudi fascinanten vpogled v zapletenost matematike in umetnosti ter jim pomaga razumeti osnovne koncepte, ki krepi matematično razumevanje.

Fibonacci-jevo zaporedje in zlati rez: Uvajanje otrok v znane matematične koncepte, kot sta Fibonacci-jevo zaporedje in zlati rez, skozi umetnost, je lahko zeeelo zanimivo. Otroci bodo ob tem odkrili, kako tesno je matematika povezana z naravo in umetnostjo.

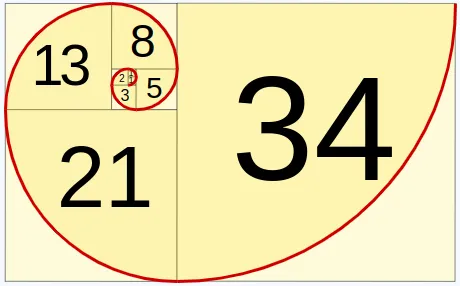
Kaj je zlati rez?

Zlat rez je posebna matematična konstanta, ki označuje idealno razmerje med dvema deloma celote, ki je estetsko privlačno. Zlat rez, označen z grško črko φ (phi), približno znaša 1,618. Zlat rez najdemo tako, da delimo dolžino v dveh delih tako, da je razmerje med celotno dolžino in daljšim delom enako razmerju med daljšim in krajšim delom.

Če dolžino (a + b) delimo na dva dela (a in b) tako, da velja:

aa+b=ba=ϕ

Potem je to razmerje približno 1,618.

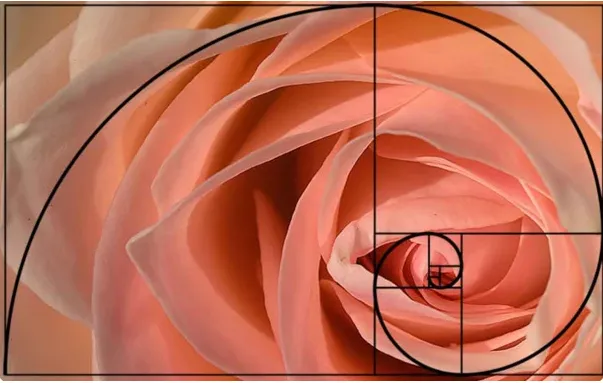
Povezava med Fibonacci-jevim zaporedjem in zlatim rezom

Zanimivo je, da se zlati rez in Fibonacci-jevo zaporedje med seboj prepletata. Če delimo zaporedna števila Fibonacci-jevega zaporedja (npr. 21/13, 34/21, 55/34), opazimo, da se približujemo vrednosti zlatega reza (1,618...). Čim dlje napredujemo v zaporedju, tem bližje so razmerja med sosednjimi števili zlategu rezu.

Svetovno znane slike in matematika za njimi

Zadnja večerja (Leonardo da Vinci)

Leonardo da Vinci je bil pionir uporabe linearne perspektive na svojih slikah. Na sliki „Zadnja večerja“ je s to matematično tehniko ustvaril občutek globine in tridimenzionalnosti. Črte prostora se zlivajo proti osrednji izginjajoči točki, kar ustvarja iluzijo oddaljenosti.

Da Vinci je pri določanju razmerij mize, položajev figur in dimenzij prostora uporabil zlato razmerje oz. zlati rez.

Zvezdnata noč (Vincent van Gogh)

V „Zvezdnati noči“ Van Gogh uporablja spirale in vrtinčaste vzorce, ki so podobni Fibonaccijevemu zaporedju, ki se pojavlja v številnih naravnih oblikah. Za to matematično zaporedje je značilna rast števil na podlagi določenega vzorca.

Rojstvo Venere (Sandro Botticelli)

Botticellijeva kompozicija Venere pogosto pooseblja proporce zlatega pravokotnika, oblike, ki je tesno povezana z zlatim rezom. Na ravnovesje in harmonijo na tej sliki so vplivala matematična načela.

Vztrajnost spomina (Salvador Dalí)

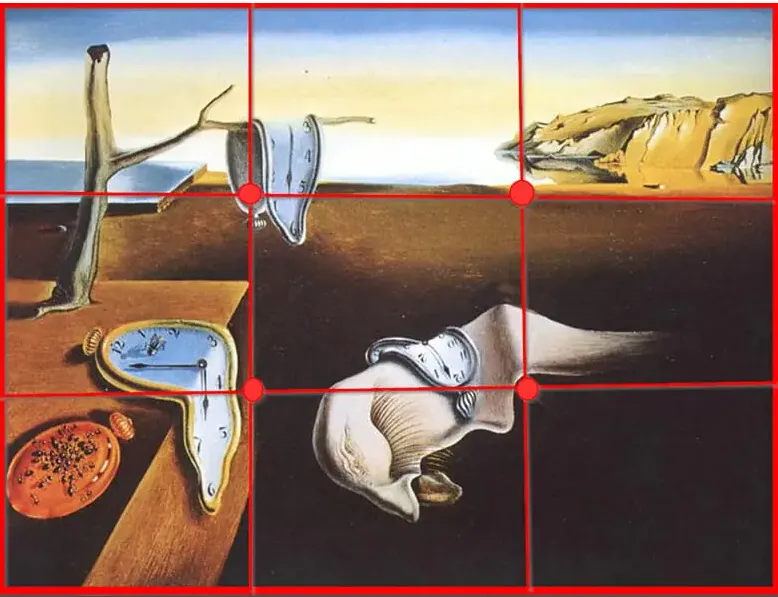
Dalíjeve ure, ki se talijo v tej nadrealistični mojstrovini spominjajo na koncept neevklidske geometrije, kjer je prostor dojet na popačen ali nekonvencionalen način. Na to idejo so baje vplivale matematične teorije Alberta Einsteina.

Guernica (Pablo Picasso)

Picassov razvoj kubizma je vključeval dekonstrukcijo oblik v geometrijske oblike, kar ponazarja matematični pristop k upodabljanju. Uporaba več perspektiv in razdrobljenih oblik izpodbija tradicionalne predstave o prostorski predstavi.

Kompozicija z rdečo, modro in rumeno (Piet Mondrian)

Mondrianova uporaba natančnih linij, pravih kotov in osnovnih barv odraža povsem matematični pristop k abstraktni umetnosti.

Vsi zgornji primeri kažejo, da so umetniki dejansko črpali navdih iz matematičnih konceptov pri ustvarjanju nekaterih najbolj ikoničnih in vplivnih umetniških del v zgodovini.

Z razumevanjem geometrije, proporcev, perspektive in drugih matematičnih načel so lahko ti umetniki svojim umetninam vdahnili drug nivo natančnosti, uravnoteženosti in vizualne privlačnosti, ki nas še danes navdihujejo.

Kakorkoli že, prepletanje umetnosti in matematike spodbuja otroško kreativnost, prav tako pa krepi tudi njihove kognitivne sposobnosti in pripravlja temelje za bolj kompleksno matematično razmišljanje v prihodnosti.

S tem, ko starši in učitelji otroke spodbujajo k raziskovanju povezav med umetnostjo in matematiko, imajo otroci priložnost, da nevede razvijajo svojo ljubezen do umetnosti in budijo radovednost in navdušenje nad matematiko.

VPIS V SPLETNO ŠOLO RISANJA ZA OTROKE

VPIS V RISKOV ATELJE - tedenske 1-urne delavnice risanja za otroke